戏说PID
Rq-Rm 于 2014-5-24 21:09 编辑
上一总结了mpu6050http://geek-workshop.com/thread-9146-1-1.html这里了解一下PID算法
对于PID算法一本书也讲不完,再说我也不懂,这里只是现学现卖简单介绍一下,
其中不明或错误之处欢迎指出,PID顾名思义……往下看吧(对于很多公式我只想说:不明觉厉!)
<备注:虽然我没有用拉氏变换讲PID,但微积分的概念是必须了解的,忘记的话不用看高数,翻一翻高中数学书就行了,里面确实有讲到>
(备注:下面很多公式等号左边的都没有写,不懂自己百度)
PID算法在数字计算机系统下是不能直接使用的,需要采用离散化方法,采用数字式PID,
在PID中积分微分和比例是这样计算的:
比例项就是这一刻的误差乘以一个常数所得项
积分项就是(这一刻的误差采样周期)+(上一刻的误差采样周期)+(上上一刻的误差采样周期)+……+(初始误差值采样周期)求和所得项
微分项就是(这一刻的误差减去上一刻的误差)/周期所得项
在实际应用中并非向上面写的那样,这里只是帮助理解,用的时候要知道变通
位置式PID
先看一个比较容易理解的PID算法,位置式PID控制算法,
位置式PID控制算法中离散表达式如下:
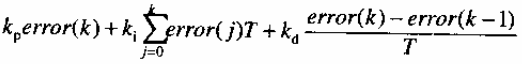
2014-4-4 12:47 上传
(8.57 KB)
至于上面式子中的字母含义我还是不说了吧,用心看会懂的,从左到右依次是比例项,积分项,微分项,
T为采样周期(就是传感器获得相邻两次数据之间的时间差),error就是想要得到的量和实际得到的量之间的差值,Kp,Ki,Kd就是所谓的PID参数,k,j,∑什么的就不要解释了吧,
位置式PID控制算法的缺点是:由于采用全量输出,所以每次输出都与过去输出有关,计算时要对误差error累加,
如果传感器出现故障偏差,计算得到的输出控制量可能出现执行机构的大幅变化,这种情况容易造成事故,
为避免这种情况发生,实际应用中以增量式PID算法居多,
增量式PID
增量式PID控制算法,
当执行机构需要的是控制量的增量时(如步进电机的驱动),应采用增量式PID控制,
既然是增量控制,那么其表达式很容易通过上面的位置式PID表达式可以推导出来:
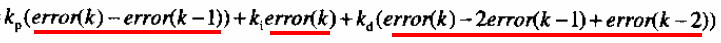
2014-4-4 12:47 上传
(9.63 KB)
对上面式子,希望不会有人做出对Ki项的疑问
显然这种方式不需要累加,控制增量之与最近的状态有关,误动作影响小,容易获得比较好的控制效果,
看完了PID的基本概念,下面分析一个实例,陀螺仪和加速计的数据融合问题
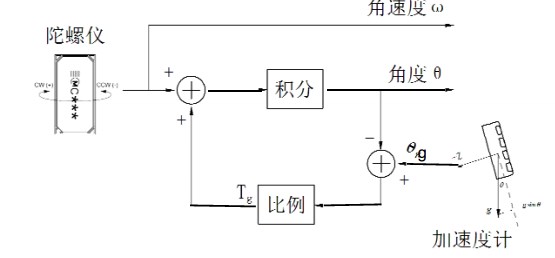
附上2011年飞思卡尔官网给出的参考方案:
陀螺仪和加速计的数据融合角度计算方案
2014-4-4 12:47 上传
(17.5 KB)
ARDUINO 代码复制打印
void CarVoltageGet(void) {long lnDeltaValue;ADC_GetValue16(g_nCarVoltage);/读取加速度值,减去零偏数值/lnDeltaValue = (int)CV_ACCE_VAL;lnDeltaValue = lnDeltaValue - (int)CV_ACCE_OFFSET;g_nCarAcceVal = (int)lnDeltaValue;/将加速度计角度归一化/g_nCarAcceVal = mult_r(g_nCarAcceVal, CV_ACCE_ANGLE_RATIO);/读取陀螺仪数值,减去零偏数值/g_nCarGyroVal = (int)CV_GYRO_VAL;g_nCarGyroVal = (int)(g_nCarGyroVal - CV_GYRO_ZERO);/归一化/g_nCarGyroVal = mult_r(g_nCarGyroVal, CAR_GYRO_RATIO_INT);/**使用一个长整型数字(g_lnCarAngleSigma)进行积分,对于数值通过右移10位(相当于除以1024)得到最终的角度值/g_nCarAngle = (int)(g_lnCarAngleSigma >> 10);lnDeltaValue = g_nCarAcceVal - g_nCarAngle;lnDeltaValue = lnDeltaValue * CAR_ACCE_RATIO;g_lnCarAngleSigma += (g_nCarGyroVal + lnDeltaValue);}void CarVoltageGet(void) {
long lnDeltaValue;
ADC_GetValue16(g_nCarVoltage);
/读取加速度值,减去零偏数值/
lnDeltaValue = (int)CV_ACCE_VAL;
lnDeltaValue = lnDeltaValue - (int)CV_ACCE_OFFSET;
g_nCarAcceVal = (int)lnDeltaValue;
/将加速度计角度归一化/
g_nCarAcceVal = mult_r(g_nCarAcceVal, CV_ACCE_ANGLE_RATIO);
/读取陀螺仪数值,减去零偏数值/
g_nCarGyroVal = (int)CV_GYRO_VAL;
g_nCarGyroVal = (int)(g_nCarGyroVal - CV_GYRO_ZERO);
/归一化/
g_nCarGyroVal = mult_r(g_nCarGyroVal, CAR_GYRO_RATIO_INT);
/*
*使用一个长整型数字(g_lnCarAngleSigma)进行积分,
*对于数值通过右移10位(相当于除以1024)得到最终的角度值
*/
g_nCarAngle = (int)(g_lnCarAngleSigma >> 10);
lnDeltaValue = g_nCarAcceVal - g_nCarAngle;
lnDeltaValue = lnDeltaValue * CAR_ACCE_RATIO;
g_lnCarAngleSigma += (g_nCarGyroVal + lnDeltaValue);
}
利用加速度计所获得的角度信息θg与陀螺仪积分后的角度θ进行比较,将比较的误差信号经过比例Tg 放大之后
与陀螺仪输出的角速度信号叠加之后再进行积分,从框图中可以看出,对于加速度计给定的角度θg,经过比例、积分环节之后产生的角度θ必然最终等于θg
由于加速度计获得的角度信息不会存在积累误差,所以最终将输出角度θ中的积累误差消除了
加速度计所产生的角度信息θg中会叠加很强的有车模运动加速度噪声信号,为了避免该信号对于θ的影响,因此比例系数Tg应该非常小
这样,加速度的噪声信号经过比例、积分后,在输出角度信息中就会非常小了
由于存在积分环节,所以无论比例Tg多么小,最终输出角度θ必然与加速度计测量的角度θg相等,只是这个调节过程会随着Tg的减小而延长
为了避免输出角度跟着θg过长,可以采取以下两个方面的措施:
(1)仔细调整陀螺仪的放大电路,使得它的零点偏置尽量接近于设定值,并且稳定
(2)在控制电路和程序运行的开始,尽量保持车模处于直立状态,这样一开始就
使得输出角度θ与gθ 相等,此后,加速度计的输出只是消除积分的偏移,输出角度不会出现很大的偏差
积分分离PID
PID之所以经久不衰,因为PID实用性很强可以千变万化来适应不同的需求,我认为很多时候并不需要高深的理论,技术上的灵活应用比一堆让人头疼的数学公式更有价值,小李飞刀独步武林大概就是这个道理,说到小李探花,这几天正是花开好时节,学校里的海棠、樱花看上去都挺好,不过桃花最艳,额……为什么陶渊明写的是桃花源记,而不是樱花海棠花呢?还有腾格尔的歌演……又闲扯了,
在普通PID算法中积分环节在启动、结束等大幅增减设定时,短时间内输出会有很大偏差,会造成PID运算的积分积累,甚至引起较大的振荡,这在实际应用中是不允许的
那么解决这种问题的一个思路就是将积分项分离开,即当被控量与设定值偏差较大时,取消积分作用,以免积分作用使系统稳定性降低;当被控量接近给定值时再引入积分控制,以便消除静差,提高控制精度;具体步骤如下:
(1)由实际情况,人为设定阀值(不知道什么是阀值?我也不知道这是谁取的名字)
(2)当误差大于阀值时采用PD控制
(3)当误差小于阀值时采用PID控制
其算法表达式如下:
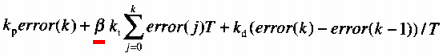
2014-4-4 12:52 上传
(7.67 KB)
其中β为积分项开关系数,即当误差大于阀值时β为0,小于阀值时β为1(阀值就是这个意思)
via - 极客工坊