四轴飞行器飞控研究(二)-姿态程序解读
本帖最后由 何处不江南 于 2015-12-10 13:23 编辑
继之前研究了一些飞行姿态理论方面的问题后,又找到了之前很流行的一段外国大神写的代码,来分析分析。
先贴上代码:
#include "AHRS.h"
//----------------------------------------------------------------------------------------------------
// Definitions
#define Kp 2.0f
#define Ki 0.005f
#define halfT 0.5f
//----------------------------------------------------------------------------------------------------
// Variable definitions
float q0 = 1, q1 = 0, q2 = 0, q3 = 0;
float exInt = 0, eyInt = 0, ezInt = 0;
//----------------------------------------------------------------------------------------------------
// Function
void AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz) {
float norm;
float hx, hy, hz, bx, bz;
float vx, vy, vz, wx, wy, wz;
float ex, ey, ez;
float q0q0 = q0q0;
float q0q1 = q0q1;
float q0q2 = q0q2;
float q0q3 = q0q3;
float q1q1 = q1q1;
float q1q2 = q1q2;
float q1q3 = q1q3;
float q2q2 = q2q2;
float q2q3 = q2q3;
float q3q3 = q3q3;
norm = sqrt(axax + ayay + azaz);
ax = ax / norm;
ay = ay / norm;
az = az / norm;
norm = sqrt(mxmx + mymy + mzmz);
mx = mx / norm;
my = my / norm;
mz = mz / norm;
hx = 2mx(0.5 - q2q2 - q3q3) + 2my(q1q2 - q0q3) + 2mz(q1q3 + q0q2);
hy = 2mx(q1q2 + q0q3) + 2my(0.5 - q1q1 - q3q3) + 2mz(q2q3 - q0q1);
hz = 2mx(q1q3 - q0q2) + 2my(q2q3 + q0q1) + 2mz(0.5 - q1q1 - q2q2);
bx = sqrt((hxhx) + (hyhy));
bz = hz;
vx = 2(q1q3 - q0q2);
vy = 2(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
wx = 2bx(0.5 - q2q2 - q3q3) + 2bz(q1q3 - q0q2);
wy = 2bx(q1q2 - q0q3) + 2bz(q0q1 + q2q3);
wz = 2bx(q0q2 + q1q3) + 2bz(0.5 - q1q1 - q2q2);
ex = (ayvz - azvy) + (mywz - mzwy);
ey = (azvx - axvz) + (mzwx - mxwz);
ez = (axvy - ayvx) + (mxwy - mywx);
exInt = exInt + exKi;
eyInt = eyInt + eyKi;
ezInt = ezInt + ez*Ki;
gx = gx + Kpex + exInt;
gy = gy + Kpey + eyInt;
gz = gz + Kp*ez + ezInt;
q0 = q0 + (-q1gx - q2gy - q3gz)halfT;
q1 = q1 + (q0gx + q2gz - q3gy)halfT;
q2 = q2 + (q0gy - q1gz + q3gx)halfT;
q3 = q3 + (q0gz + q1gy - q2gx)halfT;
norm = sqrt(q0q0 + q1q1 + q2q2 + q3q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
}
代码不长,但是数学理论基础却是十分扎实的,必须要要有之前(一)的铺垫。
一段段分析代码:
#define Kp 2.0f
#define Ki 0.005f
#define halfT 0.5f
float q0 = 1, q1 = 0, q2 = 0, q3 = 0;
float exInt = 0, eyInt = 0, ezInt = 0;
前三行是一些常数的定义,包括Kp参数,Ki参数,采样时间。
后两行是一些变量的申明,q0,q1,q2,q3分别代表四元数的4个参数a,b,c,d,v=q0+q1i+q2j+q3k
exInt,eyInt,ezInt代表误差的积分项。这个后面会有说明。
void AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz)
float norm;
float hx, hy, hz, bx, bz;
float vx, vy, vz, wx, wy, wz;
float ex, ey, ez;
来说说这些变量代表的意义,再注意各个参数是相对于哪个参考系的。这是算法理解的重点。
先说形参的
gx gy gz 表示陀螺仪读出的数据,分别为绕飞行器参考系 x轴,y轴,z轴正方向旋转的角速度。
ax ay az 表示加速度计读出的数据,分别为重力加速度在 飞行器参考系 x轴,y轴,z轴的分量。
mx my mz 表示磁场传感器读出的数据,分别为地磁场在 飞行器参考系 x轴,y轴,z轴的分量。
norm是做归一化的中间变量。
hx, hy, hz 表示将飞行器参考系上的地磁矢量转换到地理坐标系(参考坐标系)后的矢量。
bx,bz 与上面一样,(注意)区别是 bx在算法里为sqrt(hxhx+hyhy)这实际上是建立了一个误差函数,bx越接近hx,则整个估计姿态与电子罗盘测得的姿态越重合。
vx, vy, vz为将 标准单位重力 转换到飞行器参考系后 各个坐标轴上的分量。(重力加速度)
wx, wy, wz为将 bx与bz又重新 转换到飞行器参考系后 各个坐标轴上的分量。(地磁场)这个地方是比较难理解的,为什么转换过来又转换回去,后面会说。
ex, ey, ez 为向量a和向量m,与向量v和向量w的外积的在飞行器参考系的 向量。该向量描述了a和m与v和w的偏差程度。
float q0q0 = q0q0;
float q0q1 = q0q1;
float q0q2 = q0q2;
float q0q3 = q0q3;
float q1q1 = q1q1;
float q1q2 = q1q2;
float q1q3 = q1q3;
float q2q2 = q2q2;
float q2q3 = q2q3;
float q3q3 = q3q3;
这是些预先计算的数据,方便后面计算使用。
norm = sqrt(axax + ayay + azaz);
ax = ax / norm;
ay = ay / norm;
az = az / norm;
norm = sqrt(mxmx + mymy + mzmz);
mx = mx / norm;
my = my / norm;
mz = mz / norm;
对加速度传感器和磁场传感器得到的数值进行归一化,方便计算。
hx = 2mx(0.5 - q2q2 - q3q3) + 2my(q1q2 - q0q3) + 2mz(q1q3 + q0q2);
hy = 2mx(q1q2 + q0q3) + 2my(0.5 - q1q1 - q3q3) + 2mz(q2q3 - q0q1);
hz = 2mx(q1q3 - q0q2) + 2my(q2q3 + q0q1) + 2mz(0.5 - q1q1 - q2q2);
利用四元数变换坐标系。具体为什么这样变换,这里先上一张图,具体笔记一里有详细过程。传送门:笔记一http://mp.weixin.qq.com/s?__biz=MzA4MjU0MTU0NQ==&mid=402725156&idx=1&sn=b9a5cc79e822bb0a986f7b4348b86f98#rd
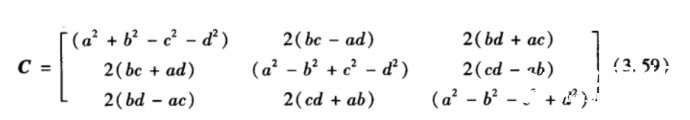
001Rju7szy6TbFtR5YV1d&690.jpg (13.54 KB, 下载次数: 4)
下载附件
保存到相册
2015-12-10 13:23 上传
上图为从飞行器坐标系转换到地理坐标系的余弦矩阵的四元数表达。
bx = sqrt((hxhx) + (hyhy));
bz = hz;
bx在当由磁场得到的飞行器参考系和由所有参数融合得到的飞行器参考系重合的时候理论上是等于hx的,此时hy应该等于0
vx = 2(q1q3 - q0q2);
vy = 2(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
反向使用上图余弦矩阵的四元数表达。及把a替换成-a,原理为四元数表达旋转时,a为旋转的角度,所以想旋转回去只需要把a变成-a。
(vx, vy, vz) 为一标准重力在飞行器参考系上的矢量。
wx = 2bx(0.5 - q2q2 - q3q3) + 2bz(q1q3 - q0q2);
wy = 2bx(q1q2 - q0q3) + 2bz(q0q1 + q2q3);
wz = 2bx(q0q2 + q1q3) + 2bz(0.5 - q1q1 - q2q2);
同理,反向使用余弦矩阵的四元数表达。
这里可能大家已经发现,wx wy wz是由磁场传感器得到的。
ex = (ayvz - azvy) + (mywz - mzwy);
ey = (azvx - axvz) + (mzwx - mxwz);
ez = (axvy - ayvx) + (mxwy - mywx);
e 为误差向量 他是 向量a和v的外积加上m和w的外积。
exInt = exInt + exKi;
eyInt = eyInt + eyKi;
ezInt = ezInt + ez*Ki;
对误差进行积分;
gx = gx + Kpex + exInt;
gy = gy + Kpey + eyInt;
gz = gz + Kp*ez + ezInt;
用误差的积分和误差本身与Kp的乘积的和对角速度进行补偿。
q0 = q0 + (-q1gx - q2gy - q3gz)halfT;
q1 = q1 + (q0gx + q2gz - q3gy)halfT;
q2 = q2 + (q0gy - q1gz + q3gx)halfT;
q3 = q3 + (q0gz + q1gy - q2gx)halfT;
利用龙格-库格法求出四元数的值,此值由补偿后的角速度求出。
norm = sqrt(q0q0 + q1q1 + q2q2 + q3q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
对四元数进行归一化。
至此算法结束。剩余的事情就是把四元数转化为欧拉角,即可求出我们可以理解的飞行器的姿态yaw,roll,pitch
另外稍微分析下这个算法的实现原理。
a与v的外积 结果为 sinθ |a||v|n n为垂直于a,v组成平面的单位向量,方向遵守右手定理。由于都是归一化的,所以,这个结果的大小与θ有关,这个θ为a与v的夹角,因为a与v在halfT时间内的区别应该非常小,所以,此时θ=sinθ,这时候可以说这个外积的每个参数与θ成正比。
这个误差是怎么来的?就是因为飞行器在这短时间旋转了一定角度。
而从另一个角度,如果单纯从陀螺仪,同样可以得到飞行器旋转的一个角度。这个时候就有个问题?我们选择相信谁的?
我们谁也不相信,而是选择按一定比例相信了3个参数,e(误差),g(陀螺仪角速度)和eInt(误差的积分),这样我们就融合了这三个参数,最终得到我们的姿态。
PS:此方式在数学上在算法上没有任何问题,但是由于地磁传感器极易受到各种干扰(想想百度地图中的指南针精确度),而此算法又将地磁传感器所指示的方向过度的融入到了姿态当中,导致实际使用中数据会非常不稳定。我也是在此之后才发现。所以之后我使用了另一种融合算法,这个留到下一次再说。
如果喜欢观看类似科技新奇事物,以及了解创客圈最新资讯,或者您对Arduino有所耳闻,可以关注扫描以下二维码,一定会带给您最新的资讯,最实用的教程,以及创客最新的玩意。