我的自平衡小车D3——滤波算法
先放代码#include <Wire.h>
#define Acc 0x1D
#define Gyr 0x69
#define Mag 0x1E
#define Gry_offset -13 // 陀螺仪偏移量
#define Gyr_Gain 0.07 // 满量程2000dps时灵敏度(dps/digital)
#define pi 3.14159
float Com_angle;
float y1, Com2_angle;
float Klm_angle;
#define Q_angle 0.01 // 角度数据置信度
#define Q_omega 0.0003 // 角速度数据置信度
#define R_angle 0.01 // 方差噪声
float bias = 0;
float P_00 = 0, P_01 = 0, P_10 = 0, P_11 = 0;
float angleG;
long timer = 0;// 采样时间
void setup() {
sensor_init(); // 配置传感器
Serial.begin(19200);// 开启串口以便监视数据
delay(1000);
}
void loop() {
long o_timer = timer; // 上一次采样时间(ms)
float Y_Accelerometer = gDat(Acc, 1); // 获取向前的加速度
float Z_Accelerometer = gDat(Acc, 2); // 获取向下的加速度
float angleA = atan(Y_Accelerometer / Z_Accelerometer) * 180 / pi;
// 根据加速度分量得到的角度(degree)
timer = millis(); // 当前时间(ms)
float omega =Gyr_Gain * (gDat(Gyr, 0) +Gry_offset);
float dt = (timer - o_timer) / 1000.0;// 微分时间(s)
angleG = angleG + omega * dt; // 对角速度积分得到的角度(degree)
// 一阶互补算法
float K;
K = 0.075; // 对加速度计取值的权重
float A = K / (K + dt);
Com_angle = A * (Com_angle + omega * dt) + (1-A) * angleA;
// 二阶互补算法
K = 0.5;
float x1 = (angleA - Com2_angle) * K * K;
y1 = y1 + x1 * dt;
float x2 = y1 + 2 * K *(angleA - Com2_angle) + omega;
Com2_angle = Com2_angle + x2 * dt;
// 卡尔曼滤波
Klm_angle += (omega - bias) * dt; // 先验估计
P_00 += -(P_10 + P_01) * dt + Q_angle *dt;
P_01 += -P_11 * dt;
P_10 += -P_11 * dt;
P_11 += +Q_omega * dt; // 先验估计误差协方差
float K_0 = P_00 / (P_00 + R_angle);
float K_1 = P_10 / (P_00 + R_angle);
bias += K_1 * (angleA - Klm_angle);
Klm_angle += K_0 * (angleA - Klm_angle); // 后验估计
P_00 -= K_0 * P_00;
P_01 -= K_0 * P_01;
P_10 -= K_1 * P_00;
P_11 -= K_1 * P_01; // 后验估计误差协方差
Serial.print(timer);
Serial.print(",");
Serial.print(angleA, 6);
Serial.print(",");
Serial.print(angleG, 6);
Serial.print(",");
Serial.print(Com_angle, 6);
Serial.print(",");
Serial.print(Com2_angle, 6);
Serial.print(",");
Serial.print(Klm_angle, 6);
Serial.print(";"); // 输出数据
delay(50);
}
int gDat(int device, int axis) {
// 读九轴姿态传感器寄存器函数
// For Arduino, by 黑马
// 调用参数表
// type device axis
// 0 1 2
// ADXL345 Acc x y z
// L3G4200D Gyr x y z
// HMC5883L Mag x z y
// Example
// 00 #include <Wire.h>
// 01 #define Acc 0x1D;
// 02 #define Gyr 0x69;
// 03 #define Mag 0x1E;
// 04
// 05void setup() {
// 06 sensor_init();
// 07 delay(1000);
// 08}
// 09
// 10void loop() {
// 11 int Z-Gyroscope;
// 12 Z-Gyroscope = gDat(Gyr, 2);
// 13 delay(50);
// 14}
int v;
byte vL, vH, address; // 存放byte数值
if (device == Acc) address = 0x32;// ADXL345的读数地址
if (device == Gyr) address = 0xA8;// L3G4200D的读数地址
if (device == Mag) address = 0x03;// HMC5883L的读数地址
address = address + axis * 2; // 数据偏移-坐标轴
Wire.beginTransmission(device); // 开始传输数据
Wire.send(address); // 发送指针
Wire.requestFrom(device, 2); // 请求2 byte数据
while(Wire.available() < 2); // 成功获取前等待
vL = Wire.receive();
vH = Wire.receive(); // 读取数据
Wire.endTransmission(); // 结束传输
if (device == Mag) v = (vL << 8) | vH;
else v = (vH << 8) | vL; // 将byte数据合并为Int
return v; // 返回读书值
}
void sensor_init() { // 配置九轴姿态传感器
writeRegister(Acc, 0x2D, 0b00001000); // 测量模式
// 配置ADXL345
writeRegister(Gyr, 0x20, 0b00001111); // 设置睡眠模式、x, y, z轴使能
writeRegister(Gyr, 0x21, 0b00000000); // 选择高通滤波模式和高通截止频率
writeRegister(Gyr, 0x22, 0b00000000); // 设置中断模式
writeRegister(Gyr, 0x23, 0b00110000); // 设置量程(2000dps)、自检状态、SPI模式
writeRegister(Gyr, 0x24, 0b00000000); // FIFO & 高通滤波
// 配置L3G4200D(2000 deg/sec)
writeRegister(Mag, 0x02, 0x00); // 连续测量
// 配置HMC5883L
}
void writeRegister(int device, byte address, byte val) { // 写寄存器
Wire.beginTransmission(device);
Wire.send(address);
Wire.send(val);
Wire.endTransmission();
}复制代码几种滤波算法相比,卡尔曼滤波明显复杂的多,计算量增大不少,现在的程序运算+取样部分已经达到30ms左右,不知道会不会受到限制,这个先不讨论了。
采样曲线:

2012-3-23 15:08 上传(90.96 KB)
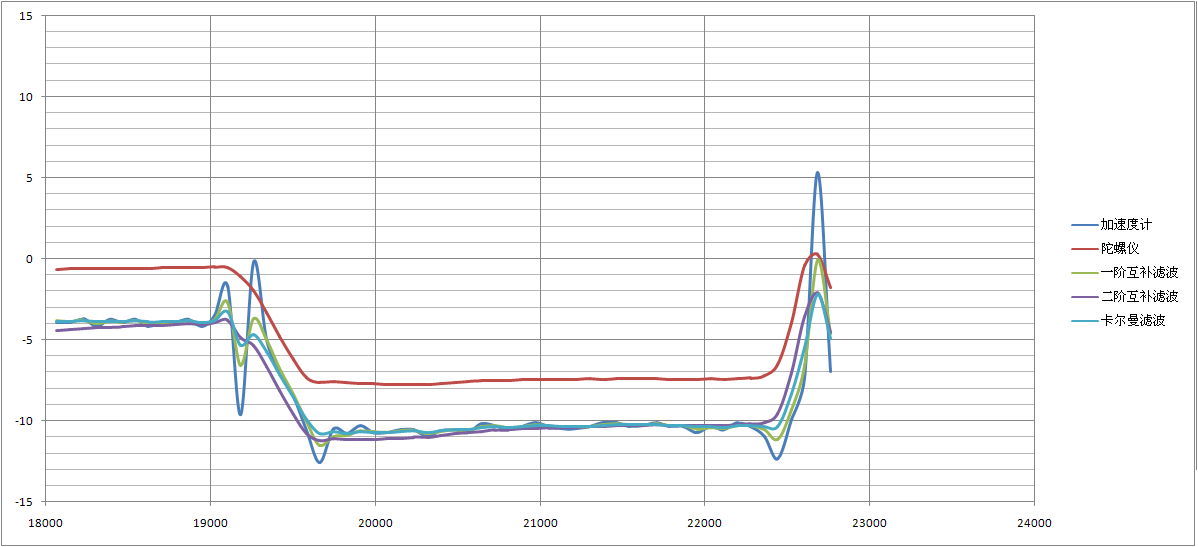
再来个局部的:
2012-3-23 15:08 上传(48.54 KB)
从曲线上看,平滑效果最好的是二阶互补滤波,但是由于K取值较小,收敛速度比较差;
卡尔曼滤波不负众望,收敛速度和滤波效果平衡得很好,或许Q_omega还可以尝试更小的值;
一阶互补滤波效果最差,但是响应还是很灵敏,K值应该还有减小的空间,而且它的运算非常简单,对采样时间几乎不构成什么影响。
三种滤波算法都可以通过调整参数得到更均衡的滤波效果,我想请教的是在这样一个没有理想曲线的情况下,有没有一个定量的方法来判定滤波特性的好坏?还是只能根据实际要求来尝试得到一个平衡值?又或对于自平衡小车和四轴飞行器,有各自的经验曲线?
via - 极客工坊